题意

给定两个长度为 $n$ 的非负整数序列 $\{a_1, \dots, a_n\}$，$\{b_1, \dots, b_n\}$。

现从中分别取出 $k$ 个数并进行两两匹配，从而分成 $k$ 对。对于一对匹配 $(a_i,b_j)$，其代价为 $|a_i-b_j|$。

你现在需要最小化各对匹配的代价之和。

对各个 $k=1,2,\dots,n$ 分别求出答案。

做法

将 $a,b$ 放在一起排序。发现要求最终答案的匹配只有不交和包含是不劣的。

这有个经典转化：把这些数划到若干层中，要求只有相同层的可以匹配。划分的方法是令第一个数在第 $0$ 层，后面每个数若和上一个数种类不同则和上一个数在相同层，若和上一个数都属于 $a$ 则在上一个数的上面一层，若都是 $b$ 就在下面那层。

我第一次见到这个套路是在这题，顺便贴个题解的图让大家理解分层方法：

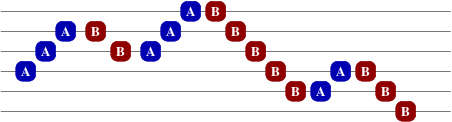
观察这种分层的方法，我们发现同一层的数必然是 $a,b$ 交替的！显然可以发现只会匹配相邻的 $a$ 和 $b$，如果产生相交或包含必然可以调整成不交使得答案更优。

对于同一层求解 $k$ 个匹配的答案是个反悔贪心的经典问题，参见【APIO/CTSC2007】数据备份。假设该层有 $k$ 个点处理该层的复杂度是 $O(k\log k)$ 的。

把每层的答案合并起来是个 $(\min,+)$ 卷积的形式。注意到每层的答案是凸的（可以费用流建模证明），直接把所有差分值放在一起升序排序就是最终答案数组的差分（即闵可夫斯基和）！时间复杂度 $O(n\log n)$。